Buffon's Needle and Noodle Problem

Recently, while flipping through a research paper made me think about the estimation of π (which we know is 3.141… ). Here is an interesting problem which is associated with a method to estimate π. A needle of length a is thrown on to the plane covered with equally spaced parallel lines with separation b. What is the probability that the needle will cross a line? How can this be extended to a random curve of length A? I thought I might just share a simple mathematical solution for both the Buffon’s Needle and Buffon’s Noodle problem that I have worked out years back on this problem during my PhD years.
The only way to do this is to illlustrate with a figure to show how a needle might land so that it just touches one of the parallels. Making use of the symmetry of the system, we only need to look at one half sgement in the diagram.The vertical position of the needle does not matter because shifting it up or down leaves the state of crossing a vertical line unchanged. The only factors which will matter will be: (a) The needle’s angle with the horizontal and (b) the distance of the centre of the needle to the nearest parallel.The centre P is equally likely to fall anywhere between the parallels, which is essentially, the assumption of uniform distribution and for a fixed angle θ, the chance that the line crosses a parallel will be
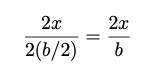
because the line crosses a parallel if the centre falls within x-units of either parallel. (See the dashed lines in the figure).
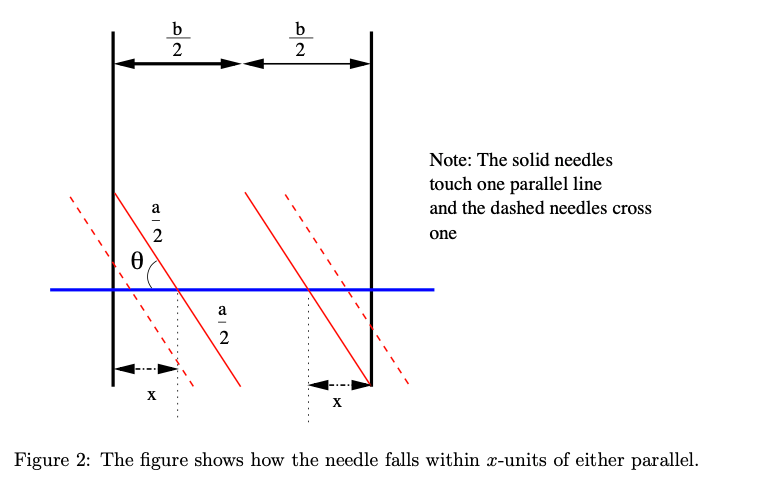
The angle θ is thought to be uniforrmly distributed from 0 to (π/2) because of twirling. The crossings that happen for θ also work for π – θ.Now we proceed to compute the probability that θ is between 0 and π/2. We need the mean value of (2x/b) for x = a/2 cos θ and it works out to be (a/b cos θ). Then integrating to find the average
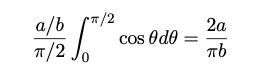
and it gives the following relation
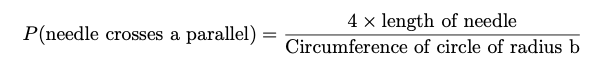
The above relation suggests a geometrical relation between a pure chance experiment and the value of the transcendental number, π, i.e. we can estimate π by tossing a long needle on a grid of squares.
We can extend the Buffon’s needle problem to Buffon’s noodle (a random curve of length A). Suppose we cut up the noodle into several needles, i.e.
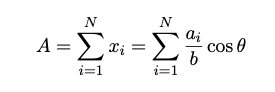
Hence, tossing the noodle is like dropping a couple of needles at one go. The equation earlier for Buffon’s needle can be extended to
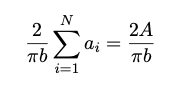
Therefore, on average, a random curve of length A is expected to intersect the lines 2A/(π b) times.
Related Links:

