The Birthday Problem

Three days ago, I discovered that one of my colleagues from Singapore Angle shares the same birthday with me. It reminded me of this interesting first year Cambridge undergraduate mathematical problem: What is the least number of persons required if the probability exceeds 0.5 that two or more persons have the same birthday (excluding the year)? So, I will offer the solution to the birthday problem (on my birthday, of course) and examine some interesting implications about the solution to this problem.

Let me start with the assumptions to solve this problem:

1. We exclude the year of birth from the date of birth in the problem. For  example, both John and Harry share the same birthday on the date 28 March.
2. We omit Februrary 29 as a possible birthday. This is easily generalized if you  want to include it. Please also omit the year from the birthday as it will complicate the problem.
3. We assume that there are 365 days for an Earth year. Let N be the number of days where you can get a birthday, and in the case that  we are living on Earth, N = 365 days, and r be the number of individuals, say r = 23,  means that there are 23 individuals.

We want to compute the probability of nobody sharing similar birthdays, P (A), hence it is obvious that the probability of getting at least one pair of birthdays, P (B), is just by taking the complement P (B) = [1 − P (A)].  Hence, for the first person, there are N days to choose from the year, and for the second person, there are (N − 1) days to pick from the year so that he or she does not share the same birthday as the first person. By induction, we conclude that for the r-th individual, he or she only has (N − r + 1) days to pick from.

Therefor the number of ways for no matching birthdays for r individuals are:  N (N − 1) . . . (N − r + 1)

To work out the probability, we need the total sample space, we need the number of ways r people can have their birthdates without restriction. There are N ways for each person. Using the multiplication principle, the total number of ways that the birthdays can be assigned to r individuals will be: N to the power of r (N^r).

We proceed to compute P (A), the probability of r individuals not sharing the same birthdays:

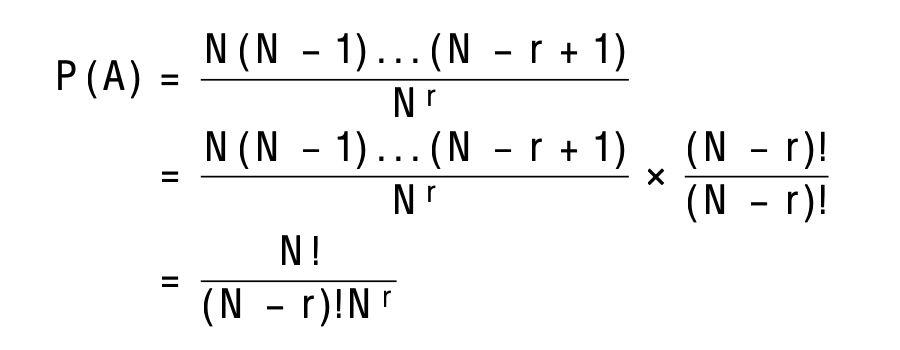
Therefore the probability of finding at least one pair of birthdays, P (B) is

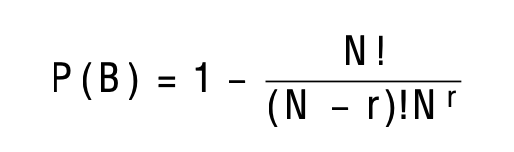
So, we solve the problem. Knowing the solution is not enough, but understanding the implication of the solution is what matters. So, let’s try to put some numbers into the equations. Let’s take N = 365 days and work out a table for different values of r (refer to table 1) .

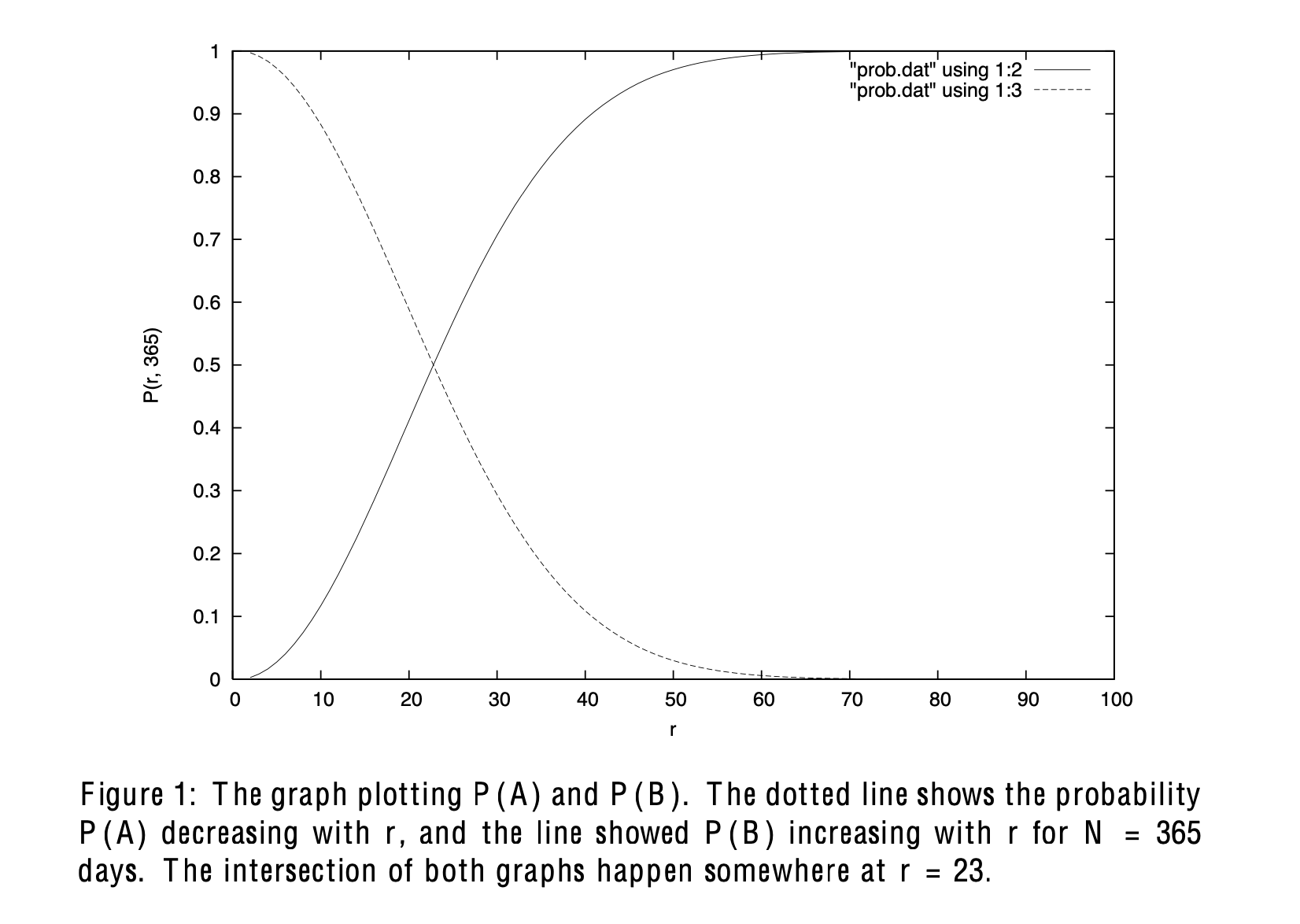
If you realize by now, the more people present in the bar, the more likely that you can find someone with the same birthday with you (excluding the year of course). It sounds counter-intuitive, but the solution is true. I thought that since there are about 50 over social-political bloggers in Singapore, the chance of finding someone with the same birthday is definitely greater than 0.5. Guess what, I found one same to mine just right next to my doorstep. Lastly, I used to tell this to my female students in Cambridge. If there is a friend coming to you making such a bet in a party with more than 100 people, don’t take the bet.